Now I can get signals into the OpenEEG modP2 format, the next stage is to qualify the filtering used within eegmir and to put an antialiasing filter in front of the ADC. The sampling rate is only 256Hz, so the highest frequency possible is 128Hz. Anything else will alias down, particularly frequencies +/- 50Hz of 256Hz, which will be aliased down to 0-50Hz and corrupt my area of interest. This includes the fourth, fifth and six harmonics of the 50Hz power frequency and the second harmonic of the 100Hz full-wave rectifier ripple tossed onto the powerline by every switched-mode power supply in the neighbourhood.
OpenEEG are good enough to put their schematic up on the Web, so I simulated their antialiasing filter.

Hmm, colour me underwhelmed. At a 10-bit resolution the steps are 1/1024, so quantisation noise is 20×log(1/1024) or about -60dBFS. So you’d like to be 60dB down at fs/2 of 128Hz, which is where I’ve drawn the line. We are at, …drum roll…, -16dB by then. At least the crap there gets aliased to the high frequencies, but by fs we are at -26dB. Nice try, but no cigar. I guess that’s the price I pay for saving myself the grunt of lining up all those analogue filters. TANSTAAFL and I get to try harder here. At least there are only two of these filters.
Elliptic filter design
The obvious way here would be to get an elliptic filter and target a notch at fs/2 and another at fs. I had thought there would be an online calculator by now, but perhaps nobody makes analogue filters any more1. So it’s back to the Williams book. It’s all about the ratio between stopband and passband. The stopband is non-negotiable at fs/2, say 120Hz so hopefully a notch will be dropping just beyond that into 128 Hz. I have flexibility on the passband, the Mind Mirror goes up to 38Hz, say I choose a passband cutoff of 60Hz, I get a steepness of 2. I’m easily prepared to take a passband ripple of 0.3dB (p=25%)2 so I am after a C ?order 25 ?theta
From Table 2-2 I want Θ=30° for my steepness of 2, so I want a C ? 25 30 filter, with only the order to determine. I’d really like that to be 3 rather than 5 😉 Sadly I look up C 03 25 283 and the stopband is only 30dB. Shifting Θ=20° would give me a steepness of 3 and a stop of 40dB, so my passband comes down to 40Hz
A C 05 25 32 would give me a stop of 60dB, I will give some of that up in component tolerances, but it’s better than 16dB and gives me some chance to fight all that mains rubbish, so let’s take a look.
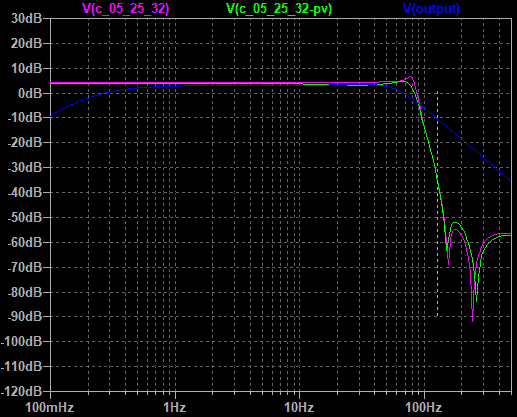
It’s not bad. I’d probably want to shift the corner frequency down by 5Hz. It’s good that it isn’t anywhere near as sensitive to component values as the Cade-Blundell bandpass ones were, the shifts due to preferred values were significant but the traces are close. For comparison the original OpenEEG line is in blue. The filter is complex, but not terrible, I can take solace that this is the quid pro quo for not having to line up all those 54 filter centre frequencies 😉

The group delay does start to increase above 60Hz, but that’s above the region of interest

So I figure I can improve the OpenEEG design and get all that mains hum and hash from aliasing into my wanted signal. When I come back to that I will tweak the corner frequency of the filter to park the second notch right on top of fs=256 Hz, it is close at 263Hz. Incoming signals at fs get aliased to fs +/- fsig, so having this notch improves my alias rejection into the frequency band of interest.
I’m glad in the end I didn’t take the easy way out and buy the OpenEEG Olimex board. I hadn’t realised that this filter needed improving. But before I construct this, however, what are the alternatives?
an introduction to Analog Front Ends via OpenBCI
How about OpenBCI? I had a hell of a job to get technical details from their website, I have the suspicion this is mainly a company to sell the hardware, they don’t really expect you to be hacking the electronics. Hacking the software, sure, effectively the hardware is a dongle for the open-source software. Anyway, they use the MCP3912 ADC and in OpenBCI_Ganglion_Library.cpp there is the line (700)
MCP_writeRegister(sampleRate); // CONFIG_0: 0x003CE050 | sample rate: 50, 100, 200, 400
so the sampling rate isn’t that different. The smart thing that is going on with the MCP3912 is that it is an oversampling converter – the default oversampling ratio is 256 times, so the analogue prefiltering only has to perform at 256x fs, even OpenEEG’s filter gets to -60dB at 1.4kHz, never mind 65kHz. It’s a better way to do that job. Maxim have a nice page on the virtues of Delta Sigma converters:
Modern Sigma-delta converters offer high resolution, high integration, low power consumption, and low cost, making them a good ADC choice for applications such as process control, precision temperature measurements, and weighing scales. Designers often choose a classic SAR ADC instead, because they don’t understand the sigma-delta types.
The analog side of a sigma-delta converter (a 1-bit ADC) is very simple. The digital side, which is what makes the sigma-delta ADC inexpensive to produce, is more complex. It performs filtering and decimation. To understand how it works, you must become familiar with the concepts of oversampling, noise shaping, digital filtering, and decimation.
This appears to be a class of ICs called Analog front Ends – according to Mouser
An Analog Front End (AFE) is used for more complex waveforms when just an analog to digital converter (ADC) is not sufficient. An AFE has a higher level of integration and includes an ADC as well as signal conditioning blocks that can include a programmable gain amplifier (PGA) and filtering circuits. It does the work of an ADC and several opamps
Digikey will sell me one for £3, but since it’s SMD I would get to lay out a circuit board and have it made for £30-odd. Not impossible but a fair amount of work and a lot of software hacking to set it up. The trouble with that higher level of integration is that these chips get obsoleted faster too, they’re designed for big consumer manufacturers pumping out a few million units or more. They don’t really care if spares are no longer available after a couple of years – Apple won’t be fixing your Iphone 7 in three years’ time. However, I do have more understanding for why OpenBCI went that way, although it means the hardware isn’t really open in practical terms. From a technical angle, however, they absolutely made the right choice – an oversampling ADC eases the analogue filtering no end, makes it smaller, all good stuff like that. So while I do take Maxim’s point, I am persisting with the skanky successive-approximation ADCs for non-technical reasons, though I tip my hat to the superiority of that approach.
This project shows I have let the grass grow under my feet somewhat…
Sadly the company I worked for moved away from electronics design in general after 2000, and this was aggravated by the process of shifting up the greasy pole, becoming more big-picture oriented. I am feeling the suckout from not working at the lab level for some time. I’ve retained all the analogue design skills but of course much more is done digitally now, and I am stuck in the mid-level microcontroller era. I am tempted to get one of these boards and learn about the DSPIC series, because I’ve always found sensors and signal acquisition and processing interesting.
A DSPIC, for instance, would probably let me sample in this project at 1024 Hz or more, then use a digital FIR filter and decimate to make the analogue antialiasing filter easier. The 16F88 hasn’t got a hope of running a FIR to do that. I’ve used the GSM data network for sending signals from remote sites like the farm network, being able to do more signal processing in the field can often reduce the data payload.
I’ve tended to favour the PICs rather than the Arduino platform, because it’s easier to get the inactive power drain down on a PIC than reduce the 7mA static load of an Arduino[ref]That’s the power drain of the Arduino with bootloader, the Atmel chip is perfectly capable of running at a lower drain in power-down mode[/ref]. The signal-to-noise ratio on Arduino forums can be tough, too, it’s sad to see EE students with less understanding of the analogue world with all the resources of the Internet than I had on leaving school just from reading books and experimentation. But I want to learn and improve my art, because there is so much more than can be done now. Investigating this project is serving me well.
- You can do this with Matlab it appears, if you have a spare £1800. That looks a lot easier then the filter table process I used ↩
- ]Electronic Filter Design Handbook, A Williams, McGraw-Hill, 1981, Table 2-3 ↩
- Electronic Filter Design Handbook, A Williams, McGraw-Hill, 1981 Table 12-57 ↩